Равномерная сходимость функциональных последовательностей и рядов

Определение. Функциональная последовательности {f_n(x)} называется равномерно сходящейся к f(x) на множестве X, если для любого ε > 0 можно указать такой номер N = N(ε) (не зависящий от x, а только от ε), что при n > N и всех x ∈ X выполняется неравенство |f(x)-f_n(x)| < ε.

Определение. Функциональная последовательности {f_n(x)} называется равномерно сходящейся к f(x) на множестве X, если ρ_n → 0 при n → ∞, где ρ_n - верхняя грань модуля разности f(x)-f_n(x) на этом множестве, то есть .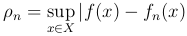

Эти два определения равномерной сходимости являются эквивалентными.

Рассмотрим сходящийся на множестве X функциональный ряд

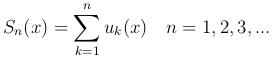
для которого S_n(x)= u₁(x) + u₂(x) + … + u_n(x), 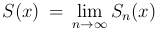. Можем записать S(x)=S_n(x)+r_n(x), тогда r_n(x)=S(x)-S_n(x). Обозначим .

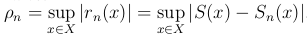Определение. Функциональный ряд называется равномерно сходящимся на некотором множестве, если последовательность его частичных сумм сходится равномерно на этом множестве.

Определение. Функциональный ряд 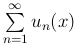называется равномерно сходящимся на множестве X, если для любого ε > 0 можно указать такой номер N = N(ε), что при n > N и всех x ∈ X выполняется неравенство |S(x)-S_n(x)| < ε или |r_n(x)| < ε.

Определение. Функциональный ряд 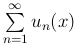называется равномерно сходящимся на множестве X, если ρ_n → 0 при n → ∞, где .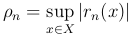

Последние два определения эквивалентны.

Признаки равномерной сходимости

Рассмотрим достаточные условия равномерной сходимости.

Теорема (Критерий Коши). Функциональный ряд 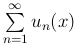равномерно сходится на множестве X тогда и только тогда, когда для любого числа ε > 0 существует такой номер N = N(ε), что при n > N, любом натуральном p и всех x ∈ X выполняется неравенство

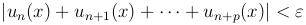
или

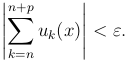
Теорема (Теорема Вейерштрасса). Если члены функционального ряда 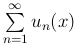определены на множестве X и по модулю не превосходят соответствующих членов сходящегося числового ряда с положительными членами 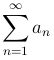(a_n > 0), то есть для всех x ∈ X

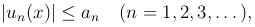
то функциональный ряд равномерно сходится на множестве X.

□ Так как ряд 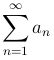сходится, то при заданном ε можно найти такое N, чтобы при всех n > N и при всех p мы имели

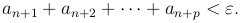
С другой стороны

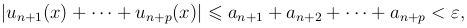
откуда и следует равномерная сходимость ряда. ■

Замечание. Функциональный ряд, удовлетворяющий условиям теоремы Вейерштрасса, называется мажорируемым, соответствующий числовой ряд называется мажорантным.

Теорема (Теорема Абеля). Функциональный ряд 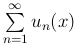сходится равномерно на множестве X, если функции u_n(x) могут быть представлены в виде

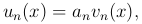
где a_n - постоянные, образующие сходящийся ряд 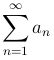, а функции v_n(x) неотрицательны и меньше постоянного положительного числа M при каждом значении x ∈ X:

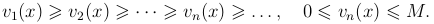
□ Положим

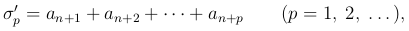
откуда следует

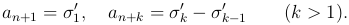
Оценим выражение

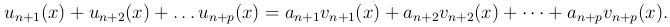
Подставляя вместо a_n+k их выражения через σ_k' и собирая члены с одинаковыми σ_k', получим

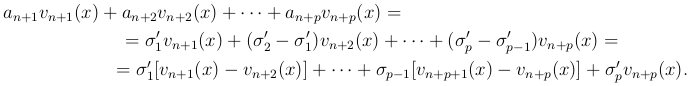
Принимая во внимание, что v_n+p(x) и все разности v_n+k+1(x) - v_n+k(x) по условию неотрицательны, можем написать

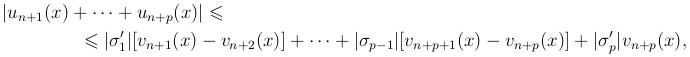
или, обозначая через σ' наибольшее из абсолютных значений |\sigma_i'|

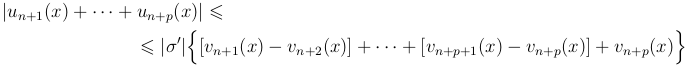
получаем, произведя сокращения,

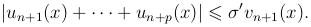
Из определения σ_k' и из сходмости ряда 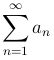следует, что для любого заданного положительного ε существует такое N, что при n > N и любом k мы имеем

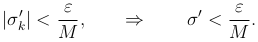
С учетом условия $0 ≤ v_n+p(x) ≤ M, получим

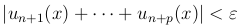
при любом n > N и при любом p. Так как N не зависит от x, то отсюда следует равномерная сходимость ряда 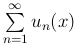на множестве X. ■

Пример. Ряды

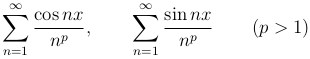
сходятся равномерно по признаку Вейерштрасса во всяком промежутке, так как при любом x имеем:

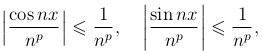
и ряд 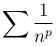при p > 1 сходящийся.

Пример. Если ряд 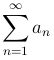сходится, то ряд

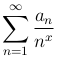
равномерно сходится в промежутке (0 ≤ x ≤ l) при любом l, так как, положив здесь

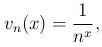
удовлетворим всем условиях признака Абеля.

Свойства равномерно сходящихся рядов

Теорема. Если ряд 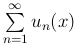сходится равномерно в промежутке X, на котором его члены u_n(x) непрерывны, то и сумма ряда S(x) непрерывна в этом промежутке.

Замечание. Доказанное утверждение можно выразить формулой

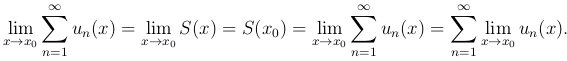
Таким образом,

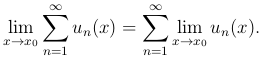
Эта формула означает, что в условиях теоремы возможен почленный переход к пределу.

Теорема. Если функции u_n(x) (n = 1, 2, 3, …) непрерывны на отрезке [a, b] и ряд 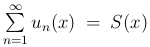сходится равномерно на [a, b], то ряд, полученный интегрированием членов данного ряда, также сходится равномерно на [a, b], причем

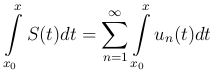
или

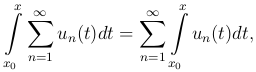
где a ≤ x₀ ≤ x ≤ b. То есть ряд можно почленно интегрировать.

Теорема. Пусть функции u_n(x) (n = 1, 2, 3, …) определены на отрезке [a, b] и имеют на нем непрерывные производные u_n'(x). Если на этом отрезке сходится ряд

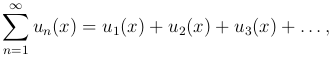
и равномерно сходится ряд, составленный из производных

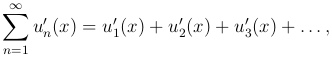
то сумма S(x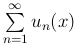) ряда имеет производную, равную сумме ряда 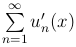, то есть

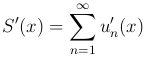
или

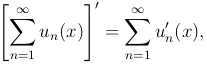
то есть ряд можно почленно дифференцировать.