Различные ряды

Рассмотрим несколько видов числовых рядов.

Определение. Гармоническим рядом называется ряд

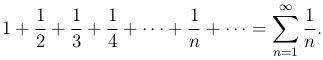
Проверим необходимый признак сходимости:

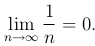
Необходимый признак выполняется, однако это не гарантирует, что ряд сходится. Сгруппируем слагаемые, начиная со второго, в группы по 1, 2, 4, ⋖ членов:

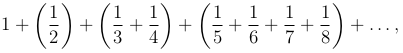
так, что в k-ой группе будет 2^k-1$ элементов. Если в каждой группе заменить все члены последним, наименьшим членом группы, то получится ряд

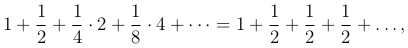сумма первых n членов которого, равная 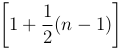, стремится к ∞ при n → ∞. Так как этот ряд расходится и соответствующие члены гармонического ряда не меньше членов этого ряда, то по первому признаку сравнения гармонический ряд также является расходящимся.

Определение. Рядом Дирихле называется ряд

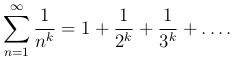
В частном случае при k = 1 ряд Дирихле совпадает с гармоническим рядом.

Определение. Рядом геометрической прогрессии называется ряд

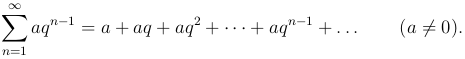
Исследуем этот ряд. Сначала мы найдем частичную сумму.

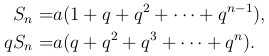
Вычитанием второго выражения из первого получим

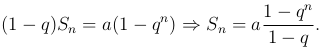
Сходимость ряда зависит от величины q:

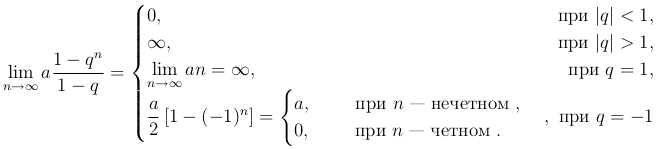
То есть ряд сходится при |q| < 1 и расходится в остальных случаях (|q| ≥ 1).