 Функции и числа
Функции и числа
 Парабола
Парабола
Запишем целую функцию n-й степени, или многочлен (полином) n-й степени:
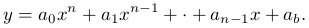
Простейший случай этого многочлена является изученная нами ранее линейная функция:
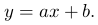
Теперь изучим трехчлен второй степени (n=2):
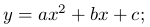
график этой функции называется параболой второй степени или просто параболой.
Начнем с простейшего случая
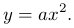
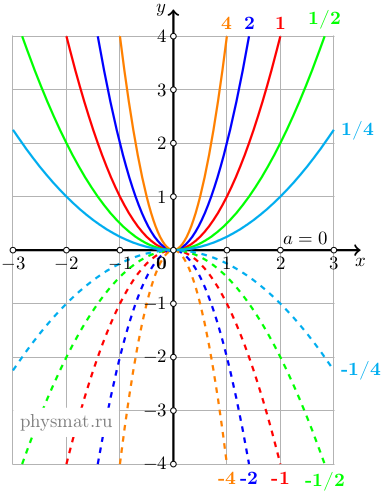
Рис. 1 График параболы второй степени y=ax² для различных a
На рисунке 1 изображен график параболы второй степени для различных значений a. Если a>0, то кривая располагается над осью Ox, а при a<0, под ней. При a=0 кривая вырождается в прямую и совпадает с осью Ox. Ордината кривой возрастает по абсолютному значению с ростом абсолютной величины x и скорость роста абсолютной величины функции увеличивается при увеличении абсолютной величины a.
Уравнение параболы не меняется если заменить x на -x, поэтому кривая при положительных значениях x является зеркальным отражением относительно оси Oy кривой при отрицательных значениях x и если точка (x, y) лежит на кривой, то точка (-x, y) также лежит на кривой. Для данной кривой ось Oy является осью симметрии параболы.
Начало координат (0, 0) является самой низкой точкой параболы при a>0 и самой высокой при a<0 и называется вершиной параболы.
Если известны координаты точки (x0, y0), лежащей на параболе, то коэффициент a однозначно вычисляется из уравнения кривой:
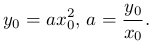
Подставив этот коэффициент в уравнение, получим уравнение параболы, проходящей через точку (x0, y0):
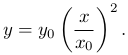
Если имеются две функции
y=f1(x), y=f2(x),
то координаты точек пересечение графиков, соответствующих этим функциям, удовлетворяют обоим функциям, а значит, их можно определить из уравнения
f1(x) = f2(x).
Рассмотрим в качества примера графический способ решения квадратного уравнения
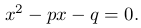
Введем две функции:
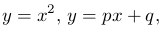
приравняв эти функции друг другу, получим квадратное уравнение. Построим график параболы и график прямой и найдем точки их пересечения. Эти точки соответствуют корням квадратного уравнения.
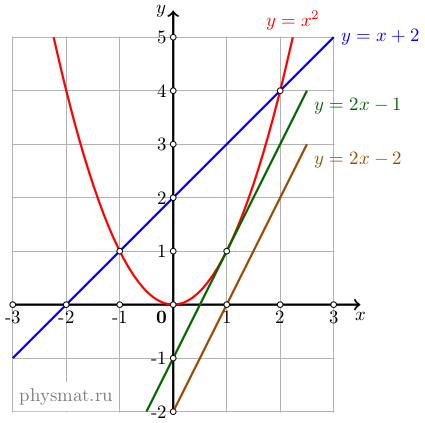
Рис. 2 График пересечения параболы второй степени y=ax² и прямой
Отметим, что прямая может пересекать параболу либо в двух точках, либо в одной, либо вообще не пересекать. Примеры для всех трех случаев показаны на рисунке 2.
Если добавить к параболе свободный член a, то график функции поднимется по оси Oy на величину a, при этом точка (0, a) будет соответствовать вершине параболы.
График для наиболее общего случая
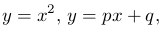
можно получить, построив графики параболы y = ax2 и прямой y = bx + c, а затем для каждого значения x просуммировать ординаты этих функций и по полученным результатам построить кривую. Пример такого построения приведен на рисунке 3.
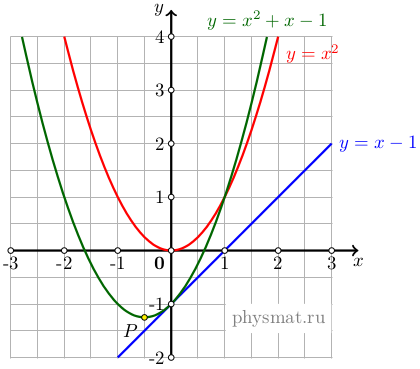
Рис. 3 Построение графика параболы второй степени в общем виде
Вершине параболы (к вычислениям этих значений мы вернемся после изучения дифференциального исчисления) соответствует точка P с координатами
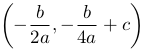
Многочлен третьей степени
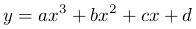
соответствует графику кривой, называемой параболой третьей степени. В простейшем случае имеем
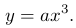
При положительных значениях коэффициента a знаки x и y одинаковые и кривая лежит в первом и третьем координатных углах, а при отрицательных a знаки x и y различаются и кривая лежит во втором и четверном квадранте. Параболы для различных значений коэффициента a приведена на рисунке 4.
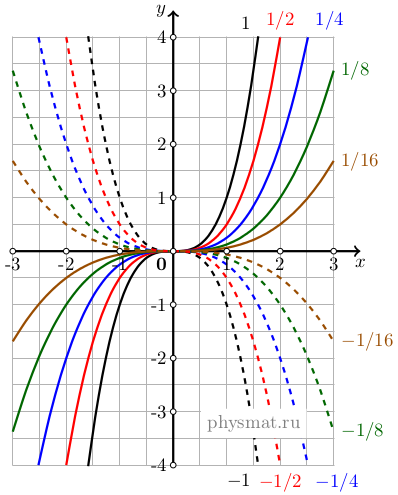
Рис. 4 График параболы третьей степени y=ax³
Одновременная замена знаков у x и y не меняет уравнение, следовательно, если точка (x, y) лежит на кривой, то и точка (-x, -y) также лежит на этой кривой, причем эти точки лежат симметрично относительно начала координат O. Отрезок соединяющие эти точки проходит через точку O разделяющую его пополам, следовательно любая хорда кривой проходящая через точку начала координат O, делится этой точкой пополам. В этом случает начало координат называют центром кривой.
Для построения параболы
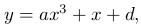
достаточно построить две кривые, параболу a x3 и прямую c x + d и взять сумму соответствующих ординат.
Отметим, что можно графически решить уравнение
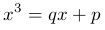
найдя точки пересечения параболы и прямой, аналогично тому, как это было описано для параболы второй степени. Парабола и прямая может иметь одну, две или три точки пересечения (рисунок 5). Доказательство того, что существует хотя бы одна точка пересечения параболы третьей степени и прямой будет приведено впоследствии.
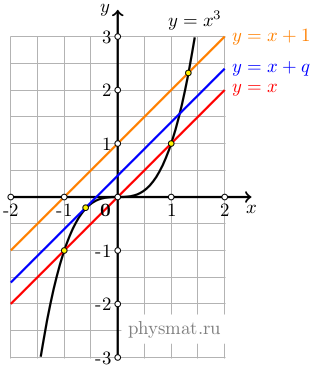
Рис. 5 График пересечения параболы третьей степени y=ax³ и прямой
Использованная литература