 Ряды
Ряды
 Теорема Дирихле
Теорема Дирихле
В данной статье ссылки на уравнения вида ( ) относятся к статье Ортогональность тригонометрических функций.
) относятся к статье Ортогональность тригонометрических функций.
Ряд Фурье функции f(x) будет сходиться и его сумма будет равна f(x), если только сделать некоторые ограничительные предположения относительно функции f(x). Мы предположим, во-первых, что функция f(x), заданная в промежутке (-π, π), или непрерывна, или имеет внутри этого промежутка лишь конечное число точек разрыва непрерывности. Мы предположим далее, что все эти точки разрыва непрерывности обладают следующим свойством: если x = c есть точка разрыва непрерывности f(x), то существуют конечные пределы f(x) при стремлении x к c: как справа( от больших значений), так и слева (от меньших значений). Эти пределы обычно обозначают f(c+0) и f(x - 0). Такие точки разрыва непрерывности обычно называют точками разрыва первого рода. Предположим, наконец, что весь промежуток (-π, π) можно разбить на конечное число частей таких, что в каждой части f(x) меняется монотонно.
Определение [Условия Дирихле]. Функция удовлетворяет условиям Дирихле в промежутке (-π, π), если она или непрерывна в этом промежутке, или имеет конечное число разрывов первого рода, и если, кроме того, промежуток (-π, π) можно разбить на конечное число таких промежутков, в каждом из которых f(x) меняется монотонно.
Заметим, далее, что на конце x = -π нам важен лишь тот предел, к которому стремится f(x) при стремлении x к -π справа, а потому вместо f(-π) мы будем писать f(-π + 0) и точно также вместо f(π) будем писать f(&pi - 0). Отметим, что пределы эти могут быть различными, но сумма ряда (1 ) должна быть, конечно, одинаковой при x = -π и x = π, в силу периодичности функций (4
) должна быть, конечно, одинаковой при x = -π и x = π, в силу периодичности функций (4 ).
).
Теорема [Теорема Дирихле]. Если f(x), заданная в промежутке (-π, π), удовлетворяет в этом промежутке условиям Дирихле, то ряд Фурье этой функции сходится во всем промежутке (-π, π) и сумма этого ряда:
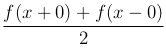
во всех точках разрыва непрерывности;
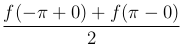
на концах промежутка, т.е. при x = -π и x = +π.
Сделаем некоторые замечания по поводу формулированной теоремы. Члены ряда (1 )суть периодические функции с периодом 2π. Поэтому, если ряд сходится в промежутке (-π, π), то он сходится и при всех вещественных значениях x, и сумма ряда периодически повторяет, с периодом 2π, те значения, которые она давала в промежутке (-π, π). Таким образом, если мы пользуемся рядом Фурье вне промежутка (-π, π), то мы должны считать, что функция f(x) продолжена во вне этого промежутка периодически с периодом 2π. С этой точки зрения концы промежутка x = ± π являются для продолженной таким образом функции точками разрыва непрерывности, если f(-π + 0) ≠ f(π - 0).
)суть периодические функции с периодом 2π. Поэтому, если ряд сходится в промежутке (-π, π), то он сходится и при всех вещественных значениях x, и сумма ряда периодически повторяет, с периодом 2π, те значения, которые она давала в промежутке (-π, π). Таким образом, если мы пользуемся рядом Фурье вне промежутка (-π, π), то мы должны считать, что функция f(x) продолжена во вне этого промежутка периодически с периодом 2π. С этой точки зрения концы промежутка x = ± π являются для продолженной таким образом функции точками разрыва непрерывности, если f(-π + 0) ≠ f(π - 0).