Ряд Фурье

В данной статье ссылки на уравнения вида () относятся к статье Ортогональность тригонометрических функций, а ссылки на уравнения вида () относятся к текущей статье.

Вернемся теперь к поставленной выше задаче. Положим, что некоторая функция f(x), определенная в промежутке (-π, π), а затем и при остальных значениях x по закону периодичности с периодом 2π, является суммою ряда 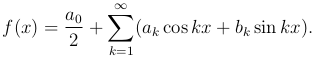(1):

(1)

Интегрируя обе части этого равенства по промежутку (-π, π) и заменяя интеграл от бесконечной суммы суммою интегралов от отдельных слагаемых, получим

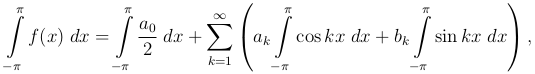
и, в силу (2), это приводится к равенству

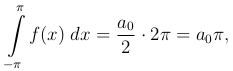
откуда определяется постоянная a₀:

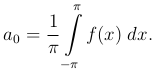
Перейдем к определению остальных постоянных. Пусть n - некоторое целое положительное число. Умножим обе части (1) на cos nx и проинтегрируем, как и выше

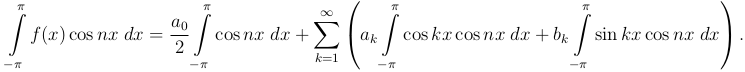(2)

В силу (2) и (3) все интегралы в правой части равенства будут равны нулю, кроме одного, а именно кроме интеграла

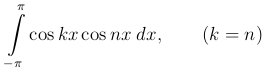а этот последний интеграл, в силу (5), будет равен π.

Формула (2), таким образом, приводится к виду

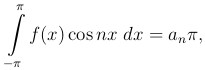
откуда

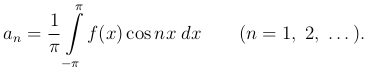(3)

Аналогично получается

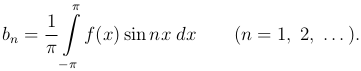
Заметим, что формула (2) совпадает с формулой (3) при n = 0. Мы можем, таким образом, написать окончательное выражение для разложение функции f(x) в тригонометрический ряд:

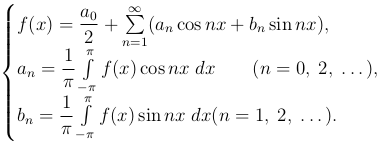(4)

Коэффициенты a_k и b_k, вычисляемые по формулам (4), называются коэффициентами Фурье функции $f(x)$, а ряд, который получается из ряда (1) после подстановки вместо a_k и b_k их значений из формул (4), называется рядом Фурье функции f(x). Операция разложения данной функции f(x) в ряд Фурье называется гармоническим анализом.

Замечание. Указанные выше формулы (3) и (5) имеют место при интегрировании по любому промежутку длины 2π. Вообще, если функция f(x), определенная при всех вещественных значениях x, имеет некоторый период a, т.е. f(x + a) = f(x) при всяком x, то интеграл от f(x) по любому промежутку длины a имеет определенное значение, не зависящее от начала этого промежутка, т.е. величина интеграла

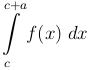
не зависит от c.

□ Действительно, число c мы можем представить в виде c = m a + h, где m - целое и h принадлежит промежутку (0, a):

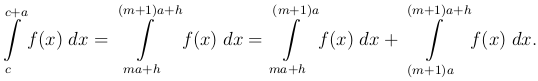
В первом интеграле введем новую переменную интегрирования t₁ = x - m a, а во втором t₂ = x - (m + 1) a:

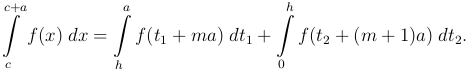
Принимая во внимание периодичность f(x) и обозначая переменные интегрирования опять через x, получим

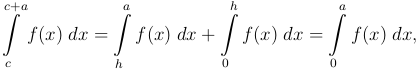
откуда и следует независимость интеграла от c. Если f(x) имеет период 2π, то мы можем вычислять ее коэффициенты Фурье a_k и b_k по формулам (4), интегрируя по любому промежутку длины 2π. ■